머신러닝 - 5. 적응형 선형 뉴런(ADALINE)

적응형 선형 뉴런이란

< 그림 1 - 버나드 위드로우(左)와 테드 호프(右) >

 

 적응형 선형 뉴런(ADAptive LInear NEuron, ADALINE, 이하 아달린)은 초창기 단일층 신경망으로써, 프랑크 로젠블랫의 퍼셉트론에 기반을 둔 좀 더 발전된 ANN(Artificial Neural Network)이 할 수 있다. 스탠포드 대학의 버나드 위드로우 교수와 그의 박사 과정 학생이었던 테드 호프가 1960년 개발하였다.

 

 아달린과 기존 퍼셉트론(멕컬록-피츠)의 차이점은 학습 방식에 있다. 아달린은 가중치를 업데이트 하는데 단위 계단 함수(Heaviside Step Function, Unit Step Function) 대신에 선형 활성화 함수를 사용한다. 아달린의 선형 활성화 함수 σ(z)는 단순 항등 함수(Identity Function)로써, σ(z) = z이다.

---

아달린의 학습 규칙

< 수식 1 - MSE를 이용하여 정의한 손실 함수 L과 예측 값  >

 

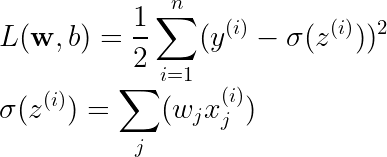
 아달린에서는 손실 함수로 MSE를 이용하고, 이의 최솟값을 구하기 위한 알고리즘으로 경사하강법을 이용한다.

 

< 수식 2 - 가중치, 편향의 변화와 변화량을 나타낸 수식 >

 

 이러한 과정을 수식으로 나타내면 위 수식 2가 되고, 이를 해석하면 가중치 w와 편향 b는 손실 함수의 미분 값의 반대 방향으로 업데이트된다는 것을 알 수 있다. 미분 값의 반대 방향으로 업데이트하는 이유는 최솟값을 구하기 위함이다(자세한 내용은 경사하강법에 대해 다룬 포스팅에서 참고). 위의 수식에서 η은 학습률(learning rate)을 뜻한다.

 

 이런 방식으로 계산한 그레디언트(손실 함수의 미분 값) 반대 방향으로 조금씩 이동하며 진행되는 방식을 완전 배치 경사 하강법(Batch Gradient Decent)이라고 한다.

 

< 수식 3 - 가중치 별 편도 함수와 절편의 편도 함수 >

 

 손실 함수의 미분 값을 구하려면, 각 가중치별 손실 함수의 편미분을 통해 편도 함수를 구해야 한다. 위의 수식 3은 수식 1에 대해서 각 가중치별 편도 함수와 절편의 편도 함수를 나타낸다. 이에 대한 증명은 꽤 복잡하기 때문에, 글의 마지막에 작성한다.

 

< 수식 4 - 아달린 학습 규칙을 나타낸 수식 >

 

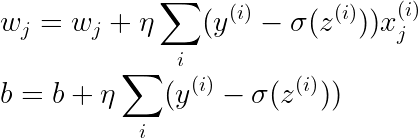
 수식 2와 수식 3을 통해, 아달린의 학습 규칙을 구할 수 있다.

---

부록: 가중치의 편도 함수 구하기

< 수식 5 - 합성함수의 미분 >

 

 가중치의 편도 함수를 구하기 이전에, 간단하게 합성함수의 미분에 대해 알아보자. 합성함수의 미분은 위 수식 5와 같이 이루어진다. 이를 이용하여 수식 2를 편미분 해보자.

 

< 수식 6 - 수식 3의 증명 >

 

 편향에 대한 편미분 과정도 위와 유사하지만, 3번째에서 4번째 식으로 넘어가는 중 미분값이 -xj가 아니라 -1이 된다는 차이점이 있다.

 

< 수식 7 - 편향에 대한 편미분 과정 중, 수식 6과 다른 부분 >