머신러닝 - 7. 로지스틱 회귀(Logistic Regression)

로지스틱 회귀란

 로지스틱 회귀(Logistic Regression)는 종속 변수와 독립 변수 간의 관계를 구체적인 함수로 나타내는 모델이다. 좀 더 자세히 설명하자면 수치형 설명변수 X와 연속형 숫자로 이루어진 종속변수 Y 간의 관계를 선형으로 가정한다. 구현하기 쉽고 선형적으로 구분되는 클래스에 뛰어난 성능을 내는 분류 모델이다. 이때, 독립 변수와 종속 변수가 각각 1개인 경우 단순 선형 회귀라고 한다.

 

 기본적으로 이진 분류를 위한 선형 모델이지만(클래스 레이블이 2개), 이 이상의 범주를 가지는 문제는 다항 로지스틱 회귀(Multinomial Logistic Regression)나 소프트맥스 회귀(Softmax Regression)으로 손쉽게 다중 클래스 설정으로 일반화할 수 있다.

 

 로지스틱 회귀는 이름에 회귀가 들어가지만, 회귀 분석과 분류 문제 모두에 사용할 수 있다.

---

로지스틱 함수

< 수식 1 - 로지스틱 함수 >

 

 로지스틱 회귀의 핵심 개념이 되는 로지스틱 함수는 위 수식 1과 같다. 이것에 대해 자세하기 설명하기 이전에, 이 함수가 어떻게 나오게 되었는지 설명할 필요가 있어 로짓 함수(Logit Function)와 오즈비(Odds, 승산)를 먼저 설명한다.

 

< 수식 2 - 오즈비(Odds) >

 

 오즈비는 위 수식 2과 같이 나타낼 수 있다. 여기서 확률 P는 어떤 일이 발생할 확률이며, 의료 분야를 예시로 든다면 양성 샘플(질병이 있는 경우) 일 확률을 이야기한다. 간단히 설명하자면 어떤 일이 발생할 확률이, 발생하지 않을 확률에 비해 몇 배나 높은가를 구한다고 할 수 있다.

 

< 수식 3 - 로짓 함수, 수식 2에 log를 취함 >

 

 위의 오즈비에다 로그 함수를 취하는 것으로, 입력 값의 범위가 [0, 1]일 때 출력 값의 범위가 (-∞, ∞ )인 로짓 함수를 정의할 수 있다.

 

< 그림 1 - 로지스틱 함수의 그래프 >

 

 실제 로짓 함수의 그래프를 그려보면, 위 그림 1과 같이 입력 값 [0, 1]에서 출력 값의 범위가 (-∞, ∞ )인 것을 알 수 있다. 이러한 로지스틱 함수를 거꾸로 뒤집으면(즉 x, y값을 뒤바꾼다면) 어떻게 되는가. 다시 말해, 로짓 함수의 역함수를 구하는 것이다.

 

< 그림 2 - 로지스틱 함수의 그래프, 로짓 함수의 역함수임 >

 

 그 경우 입력값이 (-∞, ∞ )일 때, 출력값이 [0, 1]이 되는 함수를 만들어 낼 수 있다. 위 그림 2는 수식 1의 로지스틱 함수를 그래프로 그린 것과 동일하다. 시그모이드 함수(Sigmoid Function)는 유한한 구간 (a, b)에서 항상 양의 기울기를 가지고 단조 증가하는 함수를 말한다. 로지스틱 함수를 시그모이드 함수 또는 로지스틱 시그모이드 함수라고 부르는 이유는 위 그래프를 살펴보면 알 수 있다.

 

< 수식 4 - 로지스틱 함수와 최종 입력 z >

 

 로지스틱 함수를 나타내는 수식 1에서 z는 가중치와 입력의 선형 조합으로 이루어진 최종 입력이다.

---

로지스틱 회귀 모델의 동작

< 그림 3 - 로지스틱 회귀의 동작 과정 >

 

 앞서 설명했던 로지스틱 함수는 위 그림 3의 활성화 함수에 사용된다. 가중치 w와 편향 b를 사용해 특성 x에 대한 시그모이드 함수의 출력을 내게 되면, 이는 특정 샘플이 클래스 1에 속할 확률로 해석할 수 있다.

 

< 수식 5 - 예측 확률 >

< 수식 6 - 예측 확률이 이진 출력으로 변화는 과정 >

 

 이러한 예측 확률은 임계 함수를 통해 위 수식 6과 같이, 간단하게 이진 출력으로 바꿀 수 있다.

 

< 수식 7 - 최종 입력과 출력의 관계 >

 

 따라서, 최종 입력과 출력의 관계를 수식으로 나타내면 위 수식 7과 같다.

---

로지스틱 손실 함수

< 수식 8 - 로지스틱 손실 함수 >

 

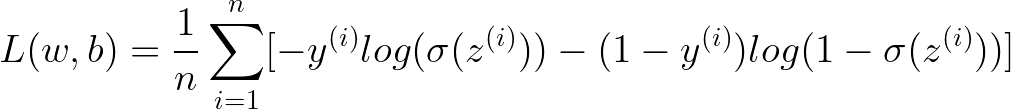
 이전 포스팅인 아달린에서 손실 함수로 MSE를 이용했던것처럼 로지스틱 회귀 모델에서도 손실 함수를 이용하는데, 여기서는 로지스틱 손실 함수를 이용한다.