머신러닝 - 8. 서포트 벡터 머신(Support Vector Machine, SVM)

서포트 벡터 머신이란

 서포트 벡터 머신(Support Vector Machine, 이하 SVM)은 주어진 데이터 집합을 바탕으로, 새로운 데이터가 어느 카테고리에 속하는지 판단하는 이진 선형 분류 모델을 만드는 알고리즘이다. 퍼셉트론이나, 아달린, 로지스틱 회귀등과의 차이점은 최적화 대상으로 마진(Margin)을 최대화한다는 것이다. 이에 대해 좀 더 자세히 알아보면 아래와 같다.

 

< 그림 1 - 세가지 초평면을 나타낸 그림(左) a와, 그중 마진이 최대화된 B를 상세하게 나타낸 그림(右) b >

 

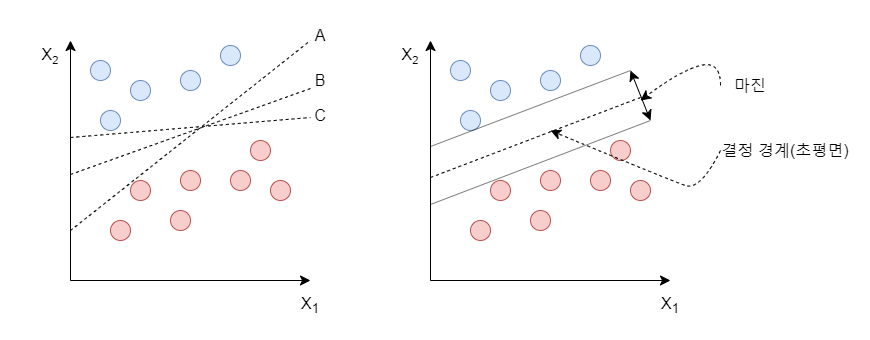
 선형 분류 모델은 클래스를 구분하는 초평면(결정 경계)으로 표현되는데, 이 초평면에 가장 가까운 훈련 샘플 사이의 거리를 마진이라 한다. 다시 말해 SVM이 마진을 최대화 한다는 것은, 앞서 말한 초평면과 가장 가까운 훈련 샘플 사이의 거리를 최대화한다는 이야기이다.

 

 위의 그림 1.a에서 세가지 초평면 중 어느 것이 가장 적절하게 두 클래스를 구분하느냐 물었을 때, 일반적으로 B가 가장 적절하게 데이터를 구분하는 초평면이라 할 수 있을 것이다. 일반적으로 마진이 크면 클수록, 새로운 데이터에 대해 오류가 발생할 가능성이 낮기 때문이다.

---

소프트 마진 분류

< 그림 2 - 데이터에 이상치가 없는 a와, 이상치가 존재하는 b >

 

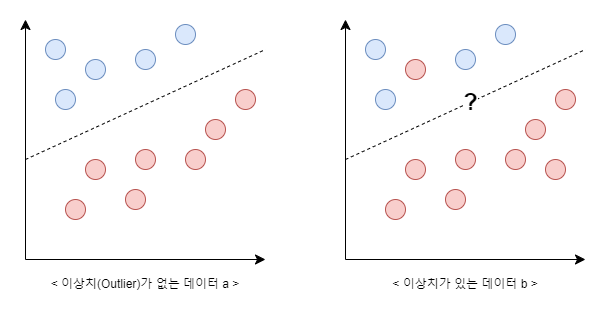
 위 그림 2.a와 같이 모든 샘플이 결정 경계를 기준으로 분류된다면 하드 마진 분류라고 한다. 그러나 모든 데이터가 이런식으로 분류되지 않는다. 그림 2.b와 같이 이상치(Outlier) 내지는 소음(Noise)이 있는 경우 하드 마진을 찾을 수 없으며, 설령 존재한다 하더라도 제대로 일반화가 이루어지지 않는다.

 

< 그림 3 - 이상치가 있는 데이터에 소프트 마진 적용 >

 

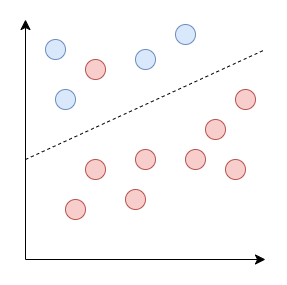
 이러한 방식으로 SVM의 최적화 목적 함수에 있는 선형 제약 조건을 완화하기 위해 도입되는 것이 슬랙 변수이다. 슬랙 변수는 모델이 훈련 데이터에 과적합하지 않도록 규제의 정도를 조절하는 변수이다. 이 값이 작으면 규제가 커져 분류 오차에 덜 엄격해져 상대적으로 큰 마진의 크기를 가지고, 이 값이 커지면 상대적으로 작은 마진의 크기를 가지게 된다.

---

커널 SVM

< 그림 4 - 선형 결정경계로 구분할 수 없는 데이터(左)와 커널을 통해 두 데이터를 구분하는 초평면을 찾은 경우(右) >

 

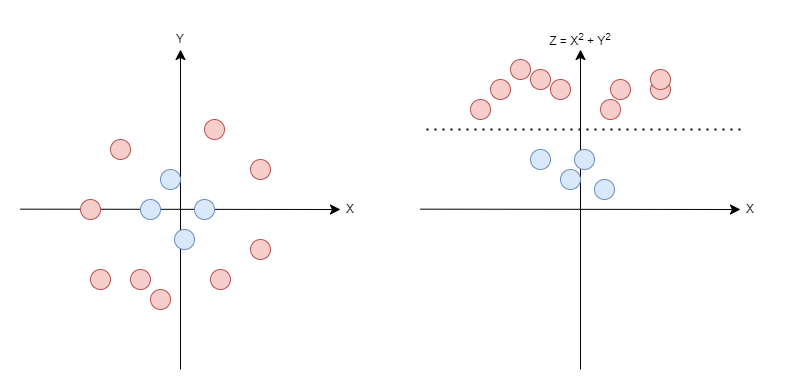
 위 그림 4와 좌측과 같은 데이터에서는, 선형의 결정 경계로 두 클래스를 구분 지을 수 없을 것이다. 이런 경우에 사용하는 방법이 커널 방법(Kernel Method)이다. 이때 말하는 커널 방법은, 원본 특성을 고차원 공간으로 투영하는 것이다.

 

 위 그림에서는 z라는 새로운 특성을 만들어냈는데, 이는 X^2 + Y^2 이다. 이렇게 (X, Y)의 2차원 특성공간을 (X, Y, Z)와 같은 3차원의 새로운 특성 공간 또는 위 그림과 같은 (X, Z)라는 새로운 특성 공간으로 변환함으로써, 두 클래스를 구분할 수 있게 된다. 이렇게 원본 특성을 고차원 공간에 투영하는 함수를 매핑 함수 Φ라 부른다.

 

 널리 사용되는 커널 함수(Kernel Function) 중 하나는 가우스 커널(Gaussian Kernel)이다. 이는 방사 기저 함수(Radial Basis Function, RBF)라고도 불리운다.