2024. 1. 16. 18:15ㆍ인공지능/머신러닝 이론
결정 트리
결정 트리는 의사 결정 규칙과 그 결과들을 트리 구조로 도식화한 의사 결정 지원 도구의 일종이다. 이는 회귀와 분류 모델 모두에 사용할 수 있다.
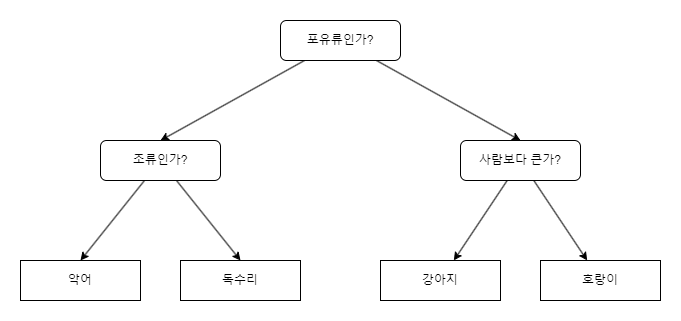
결정 트리라는 이름에서 알 수 있듯, 일련의 질문에 대한 결정을 통해 데이터를 분해하는 모델이다. 위 그림 1을 보면 쉽게 이해할 수 있다. 특성에 대한 질문을 통해 포유류와 비 포유류로 나누고, 다시 나머지들에 대한 질문이 진행된다. 스무고개 같은 느낌으로 진행된다 할 수 있다.
이러한 단계에서 가장 처음 노드인 '포유류인가?'는 루트 노드(Root Node), 가장 말단에 있는 '악어', '강아지'등은 리프 노드(Leaf Node) 내지는 터미널 노드(Terminal node)라고 부른다. 중간에 있는 분기점들인 '조류인가', '사람보다 큰가'등은 intermdediate node(중간 마디)라고 한다.
동작 과정
결정 트리는 최대한 불순도가 낮아지는 방향으로 데이터를 나누려고 한다. 이는 쉽게 말해서 특정 노드에서, 어떤 클래스에 속하는 샘플의 비율이 다른 클래스에 속하는 샘플의 비율에 비해 많이 높아지는 방향으로 데이터를 나누려고 한다는 이야기이다.

위 그림 3에서 A와 B 중에서 어느 것이 더 적절하게 데이터를 구분하였는가 생각해 보면, 직관적으로 A가 더 적절하다는 것을 알 수 있을 것이다. 왜냐하면 A의 경우 붉은색 클래스 샘플들만 한 번의 질문으로 구분해 냈기 때문이다. 이것을 A가 B보다 정보 이득(Information Gain)이 높다고 표현할 수 있다.
정보 이득을 구하기 위해 특정 클래스 샘플의 비율을 나타내는 지표인 불순도(impurity)를 사용하며, 이러한 불순도를 수치적으로 나타내는 방법 중 엔트로피(Entropy) 지수등 있다. 이 과정에 대한 상세한 내용은, 다음 절에서 설명하도록 한다.

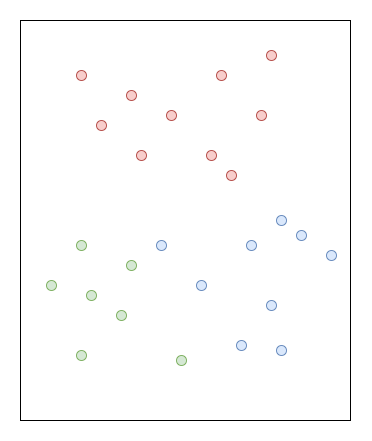
상기한 방식대로 계속해서 질문을 반복하고 데이터를 분류해 나가는 알고리즘이 바로 결정 트리 알고리즘이다. 그런데 위의 그림 4의 좌측과 우측 중에서 어느 것이 더 적절하게 데이터를 분류한 것일까? 가령 좌측 그림을 기준으로 푸른색 영역에 포함되어 있는 하나의 초록색 클래스 샘플이 이상치라면, 우측으로까지 분류할 필요가 없을 것이다.
실제 데이터에서는 이 글에서 다루는 예제 이상으로 굉장히 복잡한 데이터 셋이 주어질 것이다. 이런 경우 모든 샘플들을 깔끔하게 각 클래스별로 나누기까지(이것을 리프노드가 순수해졌다고 한다) 계속해서 작업을 반복하여, 매우 많은 노드가 생성될 것이다. 이 경우, 해당 샘플에만 잘 작동하는 과대적합이 일어날 가능성이 높아진다. 그래서 보통 트리의 최대 깊이를 제한하고, 이를 가지치기(Pruning)라 한다.
정보 이득, 엔트로피 지수
정보 이득 (Information Gain)
앞서 설명했듯이 결정 트리 알고리즘은 가장 정보가 풍부한 특성으로 노드를 나누려고 한다. 해당 과정을 최적화 하기 위한 목적함수는 정보 이득이 최대가 되는 특성으로 데이터를 나눈다. 정보 이득은 분기 이전과 분기 이후의 불순도의 차이를 말한다. 쉽게 말해 불순도가 0.9인 상태에서 0.5가 되었다면 정보 이득은 0.4다.

정보 이득을 구하는 수식은 위와 같이 정의된다. IG는 정보 이득, Dp는 부모 노드의 데이터 셋, Dj는 자식 노드의 데이터 셋, I는 불순도 지표, Nj는 j번째 자식 노드의 샘플 개수를 뜻한다. 어렵게 보이지만 위에서 설명한 것과 크게 다를 것 없다.
일반적으로 파이썬에서 이용하는 라이브러리에서는 이진 결정 트리를 사용하기 때문에 자식 노드가 2개이다. 이 경우, 수식은 아래와 같이 나타나게 된다.

엔트로피 (Entropy)
정보 이득의 수식에 대해 설명할 때, 불순도 지표 I에 대해 언급했었다. 불순도는 말 그대로 얼마나 데이터에 있는 샘플들의 불순도가 높은지 나타내는 지표다. 정확히는 특정 클래스 샘플의 비율을 나타낸다. 따라서, 서로 다른 클래스의 샘플이 적게 섞여 있을수록 낮고, 높게 섞여 있을수록 높다. 이에 대비되는 개념으로 순도(Purity)가 존재하는데, 이는 불순도의 반대 값이다. 불순도를 수치적으로 나타내는 방법에는 지니 불순도/지니 계수(Gini Impurity/Gini Index), 분류 오차, 엔트로피(Entropy)가 있다. 이 중 엔트로피는 정보의 불확실함의 정도를 나타낸다.

엔트로피를 계산하는 수식은 위와 같다. 여기서 pi는 i 클래스/범주 에 속하는 샘플의 비율을 뜻한다. 엔트로피가 0이면 불순도가 최소라는 의미이고, 엔트로피가 1일 때(서로 다른 데이터가 정확히 반씩 존재할 때) 불순도가 최대이다. 이것만으로는 정확히 이해하기 어려우므로 아래의 그림과 함께 설명한다.
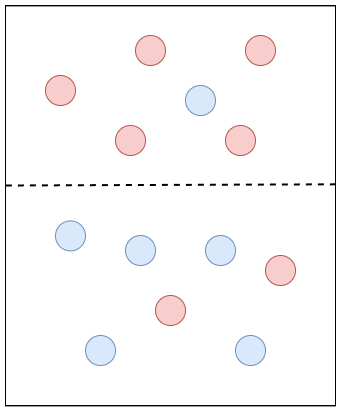
위의 그림 5의 분할하기 이전의 전체 영역에 대한 엔트로피를 구하는 방법은 다음과 같다.
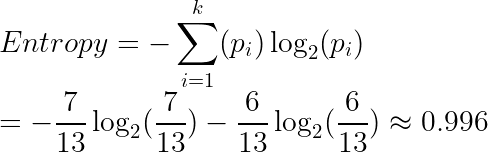
같은 방식으로 위쪽 영역의 엔트로피와 아래쪽 영역의 엔트로는 다음과 같이 구할 수 있다.

이 값들을 이용해 정보 이득을 계산할 수 있다.

지니 불순도 (Gini Impurity)

지니 불순도 또한 엔트로피처럼 불순도의 정도를 나타내는 방법 중 하나다. 잘못 분류될 확률을 최소화하기 위한 기준으로 이용한다.

엔트로피를 설명할 때 사용했던 그림 5를 다시 활용하여 지니 불순도를 계산해 보자. 분할하기 이전의 전체 불순도는 다음과 같다.

그다음 위, 아래 영역의 지니 불순도를 각각 구하면 아래와 같다.

최종적으로 정보 이득은 아래와 같이 구해진다. 이는 엔트로피로 구하는 것과 동일하다.

파이썬에서 Scikit-Learn 라이브러리를 활용한 실제 코드 및 결과를 확인하려면 이곳으로.
'인공지능 > 머신러닝 이론' 카테고리의 다른 글
| 머신러닝 - 12. 단순 선형 회귀 (Simple Linear Regression) (0) | 2024.01.22 |
|---|---|
| 머신러닝 - 11. 랜덤 포레스트(Random Forest) (1) | 2024.01.17 |
| 머신러닝 - 9. K-최근접 이웃 알고리즘(K-Nearest Neighbor, KNN) (0) | 2024.01.15 |
| 머신러닝 - 8. 서포트 벡터 머신(Support Vector Machine, SVM) (0) | 2024.01.15 |
| 머신러닝 - 7. 로지스틱 회귀(Logistic Regression) (1) | 2024.01.11 |