2024. 11. 11. 17:43ㆍ인공지능/머신러닝 이론
비전데이터 딥러닝(Deep Learning for Computer Vision)
본 게시물은 시험공부 벼락치기를 위한 글...
시험 범위는 대략적으로
- 이미지 분류
- 선형 분류
- 손실 함수
- 최적화
- 뉴럴 네트워크
- 역전파
- ConvNet
- CNN
오늘 이미지 분류->역전파까지 공부하고, 내일 ConvNet과 CNN 공부하면 아마도 괜찮을거야
Overview
비전 딥러닝 역사
Recognition via Edge Detection (1980s)
-> Recognition via Grouping (1997)
-> Recognition via Matching (1999)
-> Face Detection (2001)
-> gradient orientation (2005)
-> ?
-> Object Recognition Problem
-> Pascal
-> ImageNet
-> Alex Net
-> GoogLeNet/VGGNet (2014)
-> ResNet (2015)
-> GANs; Generative Adversarial Networks (2017)
-> Transformers (2017)
-> ViT; Vision Transformer (2020)
-> Diffusion; DALL-E2 (2020)
학습 모델 역사
- Perceptron
-> XoR Problem (1969)
-> Neocognitron (1980): 32년 뒤의 AlexNet과 유사
-> Backprop (1986): 뉴럴 네트워크 내 가중치 계산을 위한 역전파 도입, 다층 퍼셉트론의 성공적인 학습
-> Convolutional Networks (1998): Neocognitorn과 유사한 구조에 역전파 알고리즘 적용
-> Deep Learning (2000s)
-> 2012년 이후로는 딥러닝에 대한 수요 폭발, 딥러닝은 모든 곳에 존재함
- Image Classification, Image Retrieval, Object Detection, Image Segmentation
이미지 분류 (Image Classification)
이미지 분류 데이터 셋

MNIST

- 0-9까지의 숫자를 손으로 작성한 10개의 이미지 클래스
- 28x28 grayscale image
- 50k training images
- 10k test images
CIFAR10

- 10개 클래스(airplane, automobile, bird, cat, deer...)
- 50k training images(5k per class)
- 10k test iamages
- 32x32 RGB images
CIFAR 100
- 100개 클래스
- 50k training images(500 per class)
- 10k testing images(100 per class)
- 32x32 RGB images
- 20개의 슈퍼클래스가, 각각 5개의 하위 클래스를 가짐
- 예) 수생포유류: 비버, 돌고래, 해달, 물개, 고래 / 나무: 단풍나무, 소나무, 편백나무, 은행나무, 참나무
ImageNet

- 1000개 클래스
- ~1.3M training iamges(~1.3k per class)
- 50k validation images(50 per class)
- 100k test images(100 per class)
- 이미지 사이즈는 가변하나, 보통 256x256으로 리사이징하여 학습
- 22k category 버전이 존재하나, 일반적으로 사용되지는 않음
MIT places

- 365 classes of different scene types
- ~8M training images
- 18.25k validation images(50 per class)
- 328.5k test images(900 per class)
- 이미지 사이즈는 가변하나, 보통 256x256으로 리사이징하여 학습
Nearest Neighbor Classfier
Nearest Neighbor
- First classifier
- train 함수는 모든 데이터 및 라벨을 기억
- predict 함수는 테스트 이미지와 가장 유사한 학습 이미지를 통해 라벨 예측
def train(images, labels):
# machine learning
return model
def predict(model, test_images):
# Use model to predict labels
return test_labels- 이미지의 유사도 비교는 L1 distance를 이용하여 예측


import numpy as np
class NearestNeighbor:
def __init__(self):
pass
def train(self, X, y):
""" X is N x D where each row is an example. Y is 1-dimension of size N """
# the nearest neighbor classifier simply remembers all the training data
self.Xtr = X
self.ytr = y
def predict(self, X):
""" X is N x D where each row is an example. Y is 1-dimension of size N """
# lets make sure that the output type matches the input type
Ypred = np.zeros(num_test, dtype = self.ytr.dtype)
# loop over all test rows
for i in xrange(num_test):
# find the nearest training image to the i'th test image
# using the L1 distance (sum of absolute value differences)
distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
min_index = np.argmin(distances)
Ypred[i] = self.ytr[min_index]
return Ypred- 훈련 데이터를 그대로 기억함
- 각각의 테스트 이미지에 대해서 가장 L1거리가 가까운 훈련 이미지를 찾아내고, 해당 이미지의 라벨을 반환
- N개의 예제가 존재할때의 시간 복잡도
- 훈련시간복잡도: O(1)
- 테스트시간복잡도: O(N)
- -> 실제 사용하는 환경을 생각하면, 학습에 들이는 시간적 여유는 충분하지만 테스팅은 빨라야되지만 NN은 반대임
- 따라서 좋지 않은 알고리즘이라 할 수 있음
K-Nearest Neighbors
- 위의 NN이 가장 가까운 1개를 기준으로 클래스를 예측하였다면, KNN은 가장 가까운 K개를 기준으로 클래스를 예측함
- k의 수가 많아질수록 outlier의 영향을 줄일 수 있음

- 거리 계산 함수는 2가지로 나뉘어짐

- 적절한 거리 계산법을 사용한다면 어떠한 유형의 데이터에 대해서도 K-NN을 적용할 수 있음
- KNN에 대한 개념을 직접 변수값을 조정하면서 확인하고 싶다면, 다음의 웹 사이트 참고가능
http://vision.stanford.edu/teaching/cs231n-demos/knn/
http://vision.stanford.edu/teaching/cs231n-demos/knn/
vision.stanford.edu
하이퍼 파라미터
- K의 개수, 거리 계산법의 선택 등 최선의 분류를 위해 설정해야 하는 변수가 존재함
- 이러한 훈련 데이터로부터 학습하는 것이 아닌, 초기에 설정해주는 변수를 Hyperparameters이라 함
- 하이퍼 파라미터는 문제 의존적임 <- 직접 여러 값을 테스트해가면서 데이터/작업에 대한 최적의 값을 찾아줘야 함
하이퍼 파라미터 설정

- 1. 데이터 셋 전체를 학습에 사용하면, 훈련 데이터에 최적화되어버림
- 2. 알고리즘이 새로운 데이터에 대해서 어떻게 수행될지 예측할 수 없음
- 3. 따라서, 데이터 셋을 훈련(train), 검증(validation), 테스트(test) 데이터 셋으로 나누어야 함

- Cross-Validation
- 데이터를 fold라는 단위로 나눔
- 각 fold를 검증에 사용하면서, 결과의 평균을 계산
- 작은 데이터 셋에 효과적이나, 딥 러닝에 자주 이용되지는 않음
K-NN: 보편적 근사치
- 훈련 샘플의 개수가 무한대에 가까워진다면, KNN은 어떠한 형태의 함수도 표현할 수 있음

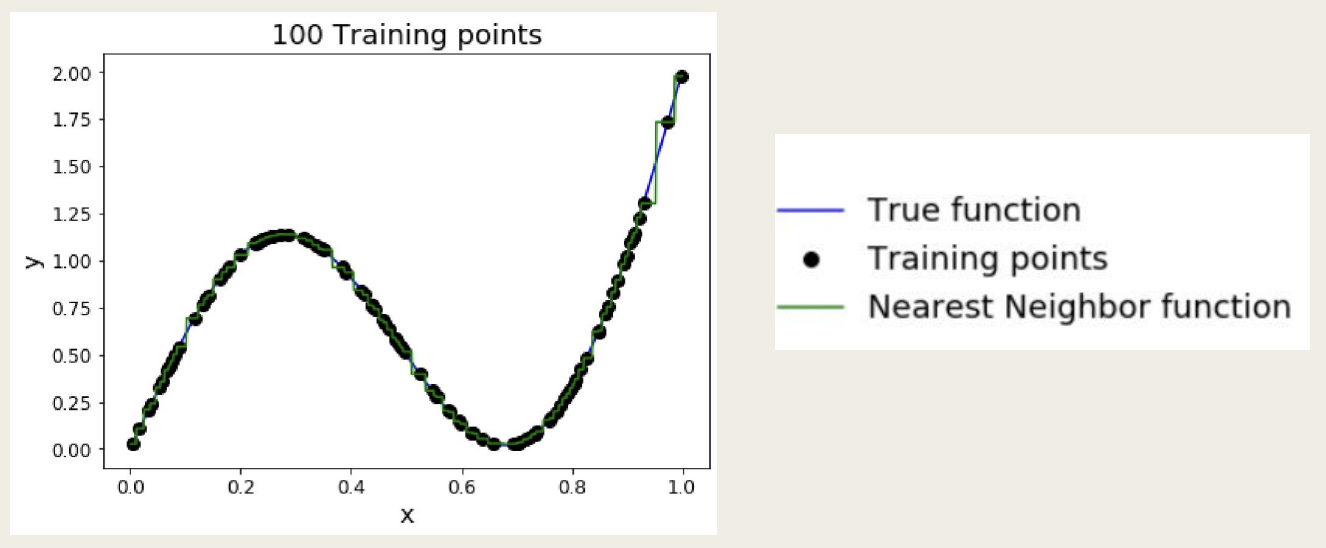
- 문제점: 차원의 저주 (Curse of Dimensionality)
- 데이터 피처 차원의 수가 늘어날수록 필요한 훈련 샘플의 수는 제곱에 비례하여 증가함
- 32x32 binary image에서 가능한 경우의 수는 2^(32x32)개, 즉 10^308개
- 우주에 존재하는 원자의 개수가 대략 10^97개라는 것을 생각하면 지나치게 많이 필요함

Linear Classification for Image
Parametric Approach
- 변수를 추출하는 것으로 분류를 시도함
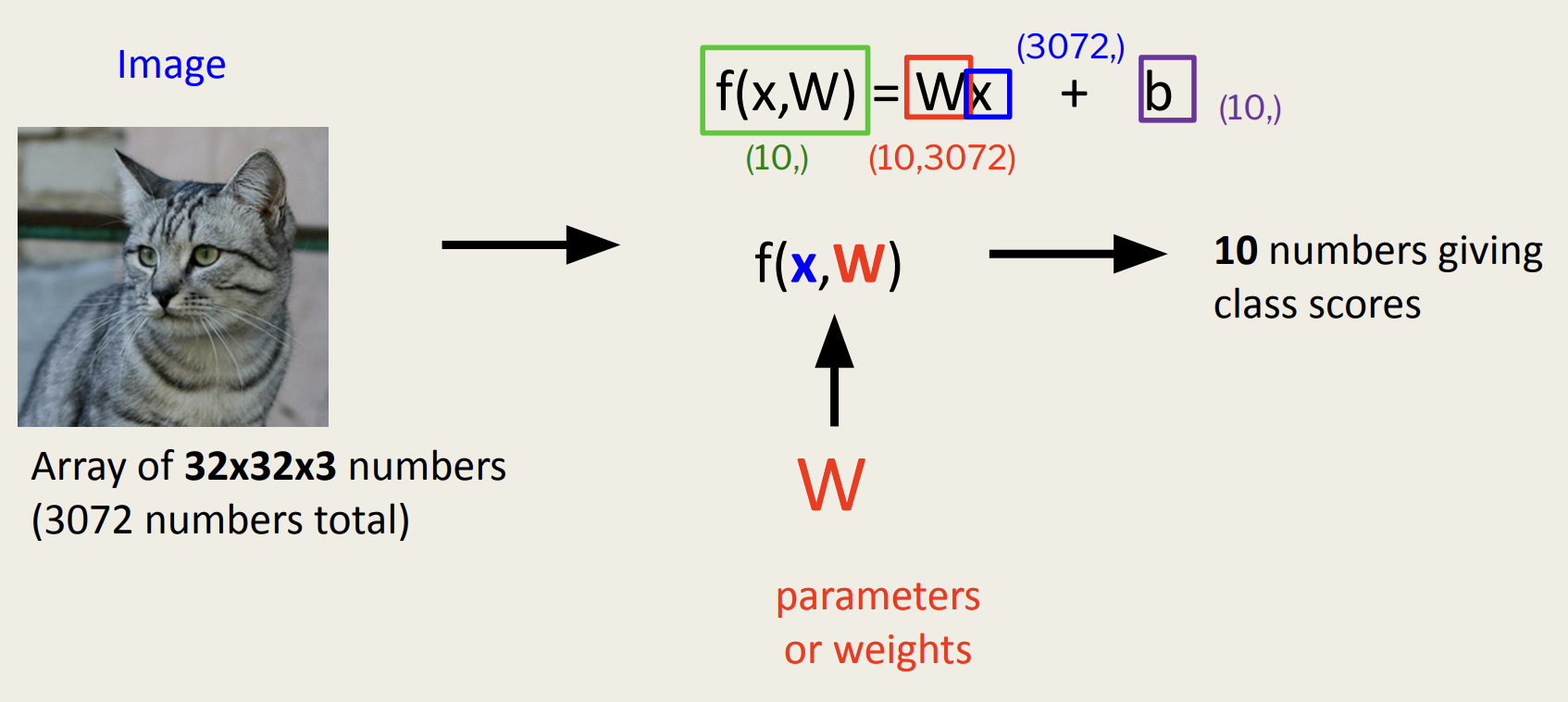
Summary

Three Viewpoints on Interpreting a linear classifier

2x2 크기의 이미지와, 3가지 클래스가 존재한다는 가정
1. 대수적 관점(Algebraic Viewpoint)
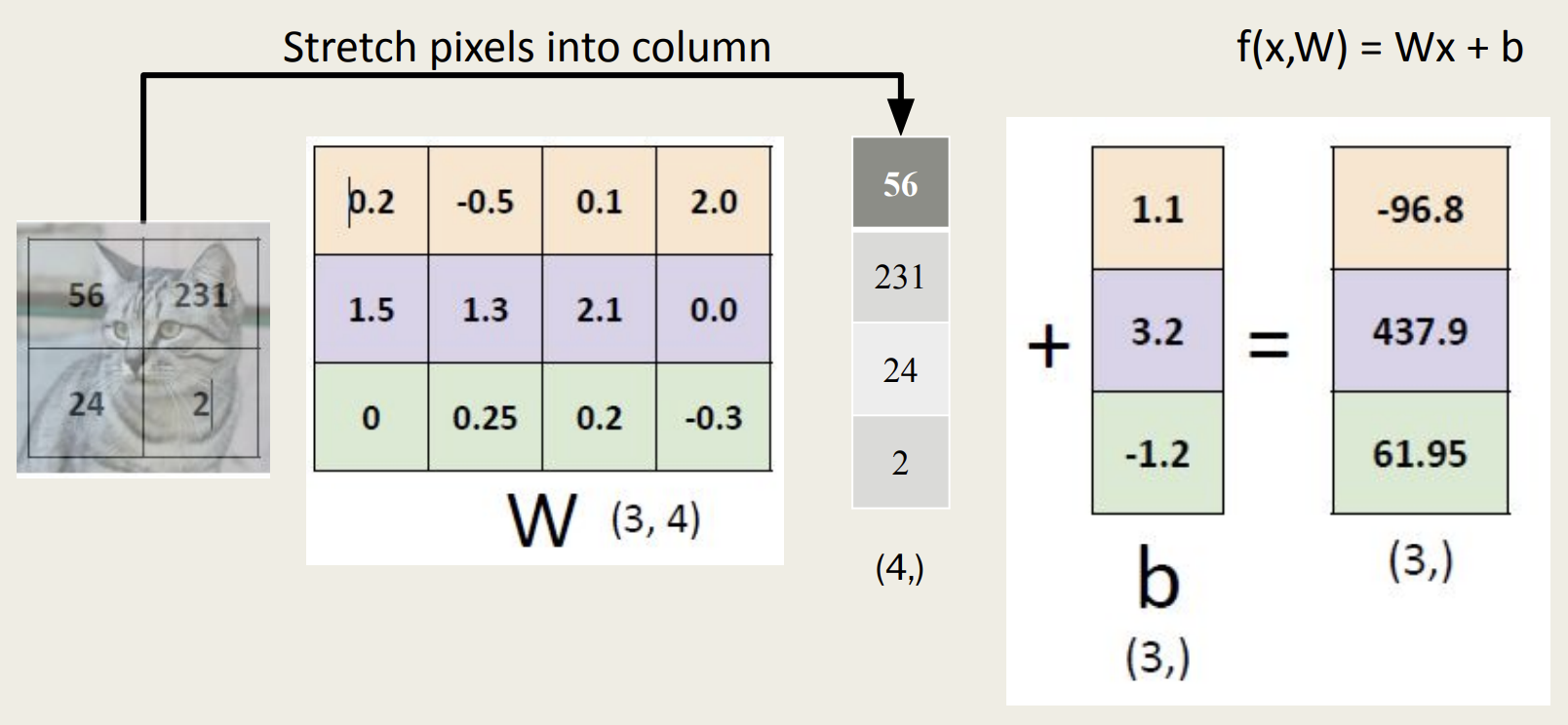

- 위 그림에서 x와 0.5 * x의 결과를 보면 확인할 있듯, 예측(결과)은 선형적임
2. 시각적 관점(Visual Viewpoint)

- 선형 분류는 카테고리 당 하나의 템플릿을 가지고 있음
- 단일 템플릿은 여러 모드의 데이터를 캡처할 수 없음
3. 기하학적 관점(Geometric Viewport)
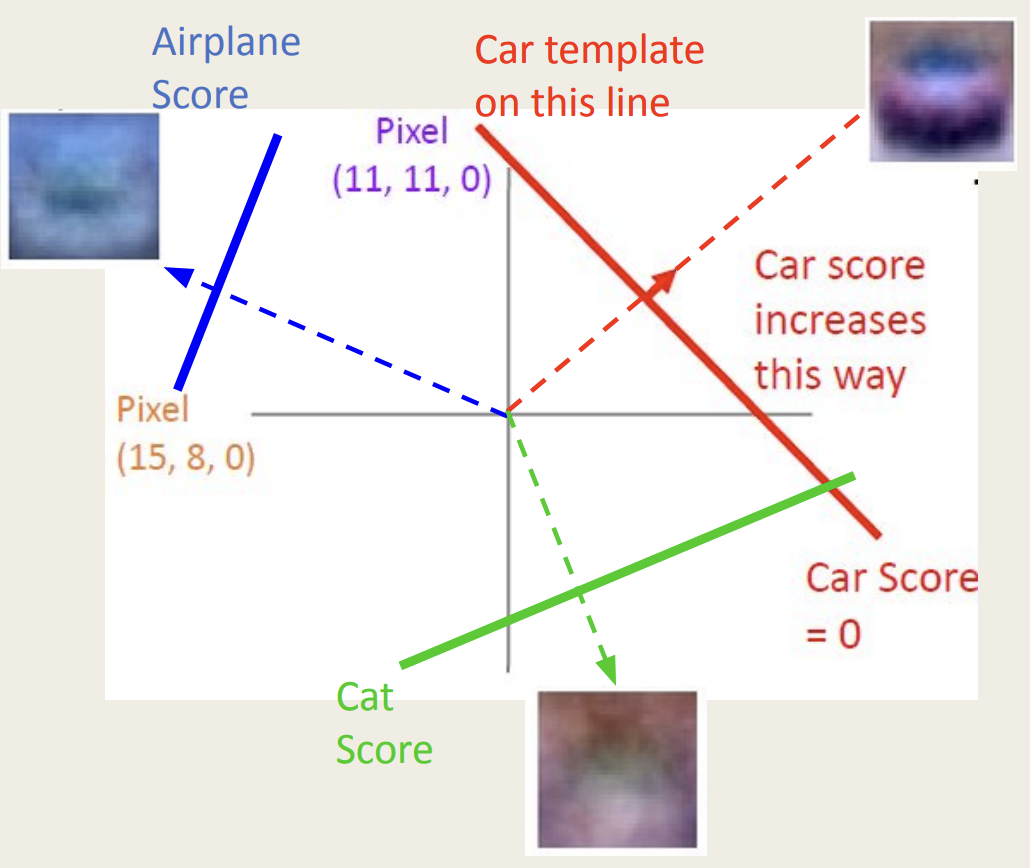
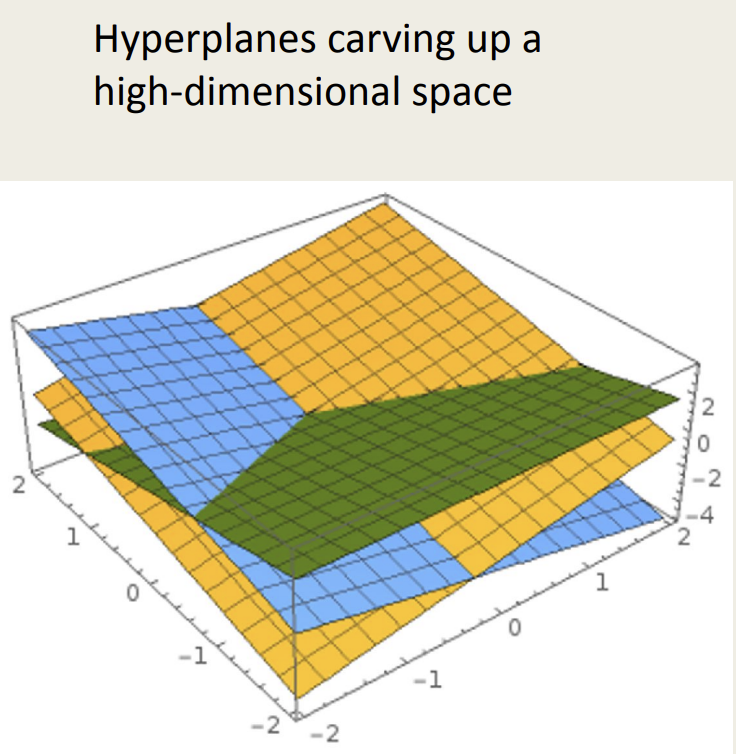
선형 분류로 분류하기 어려운 것

- 퍼셉트론은 XOR을 학습할 수 없다는 문제점 발견

'인공지능 > 머신러닝 이론' 카테고리의 다른 글
| 머신러닝 - 12. 단순 선형 회귀 (Simple Linear Regression) (0) | 2024.01.22 |
|---|---|
| 머신러닝 - 11. 랜덤 포레스트(Random Forest) (1) | 2024.01.17 |
| 머신러닝 - 10. 결정 트리 (Decision Tree) (0) | 2024.01.16 |
| 머신러닝 - 9. K-최근접 이웃 알고리즘(K-Nearest Neighbor, KNN) (0) | 2024.01.15 |
| 머신러닝 - 8. 서포트 벡터 머신(Support Vector Machine, SVM) (0) | 2024.01.15 |